An Overview of Epistemic Uncertainty in Deep Learning

There’s a basic understanding that when out-of-sample pictures are fed to a deep studying classifier, the mannequin nonetheless makes an attempt to categorise the picture as a member of one of many courses current in it is coaching set; at this level aleatoric/information uncertainty units in.

Now contemplate a state of affairs the place edge instances of pictures current within the coaching dataset are fed to the mannequin. On this case, the mannequin makes an attempt to categorise the picture as normal nevertheless it undoubtedly might be much less sure. How will we understand this type of uncertainty? On this article we might be making an attempt to just do that within the context of picture classifiers.

import torch
import torch.nn as nn
import torch.nn.useful as F
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as Datasets
from torch.utils.information import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
import cv2
from tqdm.pocket book import tqdm
import seaborn as sns
from torchvision.utils import make_grid

if torch.cuda.is_available():
  system = torch.system('cuda:0')
  print('Working on the GPU')
else:
  system = torch.system('cpu')
  print('Working on the CPU')

Epistemic/Mannequin Uncertainty

Epistemic uncertainty happens when a deep studying mannequin encounters an occasion of information which it ought to ordinarily have the ability to classify however it may’t probably be fairly sure resulting from an insufficiency of comparable pictures within the coaching dataset.

In easier phrases, contemplate a mannequin constructed to categorise vehicles. The coaching dataset is full of vehicles of various courses from quite a lot of angles, let’s assume that the mannequin is then provided a picture of a automobile flipped on it is aspect at inference time; sure the mannequin is constructed to categorise vehicles and sure, the mannequin will present a classification for that exact flipped automobile, however the mannequin had not come throughout a flipped automobile at coaching time so how dependable will that exact classification truly be?

An Not sure Mannequin

Relating to classifiers their outputs usually are not precisely a measure of certainty of a knowledge occasion belonging to a selected class, they’re extra of a measure of similarity or closeness to a selected class. As an illustration, if a cat and canine classifier is feed a picture of a horse and the mannequin predicts that picture to be 70% cat, the mannequin merely implies that the horse seems to be extra catlike than doglike. That individual classification is predicated on the parameters of the mannequin as optimized for that particular structure.

Armed with this data we are able to start to comprehend that maybe if one other cat-dog classifier had been to be educated, attaining related accuracy as the primary mannequin, it’d suppose the horse picture is extra doglike than catlike. The identical factor applies to edge pictures, when totally different fashions of various architectures educated for the very same job encounter these pictures there’s a tendency to categorise them in another way as they’re all not sure of what that exact occasion of information actually is.

Bayesian Fashions

As said within the earlier part, if we prepare quite a lot of totally different fashions, say 50 as an illustration, all for a similar job after which feed the identical picture by them we are able to infer that if an amazing majority of fashions classify mentioned picture to belong to a selected class then the fashions are sure about that exact picture.

Nonetheless,  if there’s a appreciable distinction in classification throughout fashions then we are able to start to have a look at mentioned picture as one which the fashions usually are not sure about. When that is finished, it may be mentioned that we’re making a Bayesian inference on that exact picture.

Bayesian Neural Networks

We are able to all agree that coaching 50 totally different deep studying fashions is a frightening job as it’s can be each computation and time costly. Nonetheless, there’s a option to mimic the essence of a number of fashions current in a single mannequin; and that is by using an strategy known as Monte Carlo Dropout.

Dropout is often utilized in neural networks for regularization. It is working precept is hinged within the switching off of random neurons for each move by the neural community in order to create a barely deferent structure and forestall overfitting. Dropout is turned on throughout coaching however turned off at inference/analysis.

Whether it is left turned on throughout inference then we are able to simulate the presence of various architectures every time we make the most of the mannequin. That is primarily what Monte Carlo Dropout entails and any neural community used on this manner is termed a Bayesian Neural Community.

Replicating a Bayesian Neural Community

For the sake of this text, we might be incorporating dropout layers into the Lenet-5 structure in a bid to create a Bayesian neural community whist using the MNIST dataset for coaching and validation.

Dataset

The dataset to be utilized for this job is the MNIST dataset. and it may be loaded in PyTorch utilizing the code cell beneath.

#  loading coaching information
training_set = Datasets.MNIST(root="./", obtain=True,
                              rework=transforms.Compose([transforms.ToTensor(),
                                                            transforms.Resize((32, 32)),
                                                            transforms.Normalize(0.137, 0.3081)]))

#  loading validation information
validation_set = Datasets.MNIST(root="./", obtain=True, prepare=False,
                                rework=transforms.Compose([transforms.ToTensor(),
                                                              transforms.Resize((32, 32)),
                                                              transforms.Normalize(0.137, 0.3081)]))

Mannequin Structure

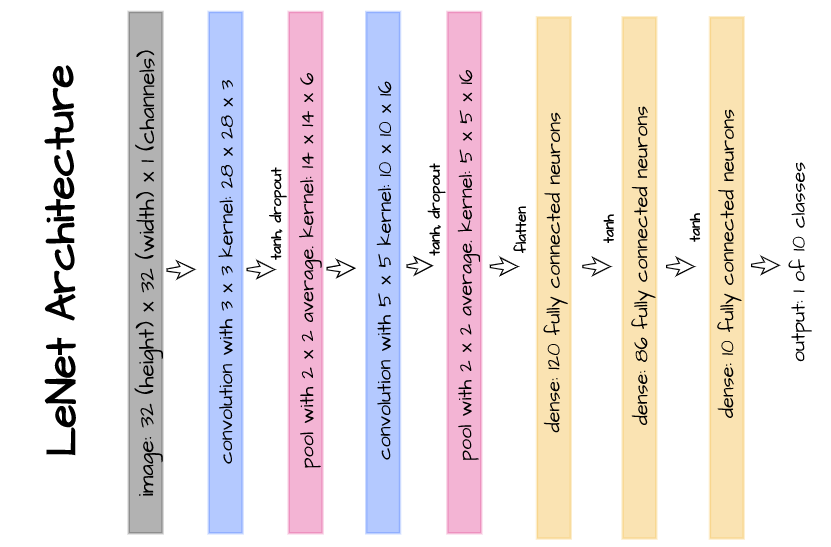
The above illustrated structure entails the usage of dropout layers after the primary and second convolution layers within the lenet-5 structure. It’s replicated within the code cell beneath utilizing PyTorch.

class LeNet5_Dropout(nn.Module):
  def __init__(self):
    tremendous().__init__()
    self.conv1 = nn.Conv2d(1, 6, 5)
    self.dropout = nn.Dropout2d()
    self.pool1 = nn.AvgPool2d(2)
    self.conv2 = nn.Conv2d(6, 16, 5)
    self.pool2 = nn.AvgPool2d(2)
    self.linear1 = nn.Linear(5*5*16, 120)
    self.linear2 = nn.Linear(120, 84)
    self.linear3 = nn. Linear(84, 10)

  def ahead(self, x):
    x = x.view(-1, 1, 32, 32)

    #----------
    # LAYER 1
    #----------
    output_1 = self.conv1(x)
    output_1 = torch.tanh(output_1)
    output_1 = self.dropout(output_1)
    output_1 = self.pool1(output_1)
    
    #----------
    # LAYER 2
    #----------
    output_2 = self.conv2(output_1)
    output_2 = torch.tanh(output_2)
    output_2 = self.dropout(output_2)
    output_2 = self.pool2(output_2)
    
    #----------
    # FLATTEN
    #----------
    output_2 = output_2.view(-1, 5*5*16)

    #----------
    # LAYER 3
    #----------
    output_3 = self.linear1(output_2)
    output_3 = torch.tanh(output_3)
    
    #----------
    # LAYER 4
    #----------
    output_4 = self.linear2(output_3)
    output_4 = torch.tanh(output_4)
    
    #-------------
    # OUTPUT LAYER
    #-------------
    output_5 = self.linear3(output_4)
    return(F.softmax(output_5, dim=1))

Mannequin Coaching, Validation and Inference

Under, a category is outlined which encapsulates mannequin coaching, validation and inference. For the inference technique ‘predict()’, analysis mode will be switched off when Bayesian inference is being sought, preserving dropout in place thereby permitting the mannequin for use for each common and Bayesian inference as desired.

class ConvolutionalNeuralNet():
  def __init__(self, community):
    self.community = community.to(system)
    self.optimizer = torch.optim.Adam(self.community.parameters(), lr=1e-3)

  def prepare(self, loss_function, epochs, batch_size, 
            training_set, validation_set):
    
    #  creating log
    log_dict = {
        'training_loss_per_batch': [],
        'validation_loss_per_batch': [],
        'training_accuracy_per_epoch': [],
        'training_recall_per_epoch': [],
        'training_precision_per_epoch': [],
        'validation_accuracy_per_epoch': [],
        'validation_recall_per_epoch': [],
        'validation_precision_per_epoch': []
    } 

    #  defining weight initialization perform
    def init_weights(module):
      if isinstance(module, nn.Conv2d):
        torch.nn.init.xavier_uniform_(module.weight)
        module.bias.information.fill_(0.01)
      elif isinstance(module, nn.Linear):
        torch.nn.init.xavier_uniform_(module.weight)
        module.bias.information.fill_(0.01)

    #  defining accuracy perform
    def accuracy(community, dataloader):
      community.eval()
      
      all_predictions = []
      all_labels = []

      #  computing accuracy
      total_correct = 0
      total_instances = 0
      for pictures, labels in tqdm(dataloader):
        pictures, labels = pictures.to(system), labels.to(system)
        all_labels.prolong(labels)
        predictions = torch.argmax(community(pictures), dim=1)
        all_predictions.prolong(predictions)
        correct_predictions = sum(predictions==labels).merchandise()
        total_correct+=correct_predictions
        total_instances+=len(pictures)
      accuracy = spherical(total_correct/total_instances, 3)

      #  computing recall and precision
      true_positives = 0
      false_negatives = 0
      false_positives = 0
      for idx in vary(len(all_predictions)):
        if all_predictions[idx].merchandise()==1 and  all_labels[idx].merchandise()==1:
          true_positives+=1
        elif all_predictions[idx].merchandise()==0 and all_labels[idx].merchandise()==1:
          false_negatives+=1
        elif all_predictions[idx].merchandise()==1 and all_labels[idx].merchandise()==0:
          false_positives+=1
      attempt:
        recall = spherical(true_positives/(true_positives + false_negatives), 3)
      besides ZeroDivisionError:
        recall = 0.0
      attempt:
        precision = spherical(true_positives/(true_positives + false_positives), 3)
      besides ZeroDivisionError:
        precision = 0.0
      return accuracy, recall, precision

    #  initializing community weights
    self.community.apply(init_weights)

    #  creating dataloaders
    train_loader = DataLoader(training_set, batch_size)
    val_loader = DataLoader(validation_set, batch_size)

    
    for epoch in vary(epochs):
      print(f'Epoch {epoch+1}/{epochs}')
      train_losses = []

      #  coaching
      #  setting convnet to coaching mode
      self.community.prepare()
      print('coaching...')
      for pictures, labels in tqdm(train_loader):
        #  sending information to system
        pictures, labels = pictures.to(system), labels.to(system)
        #  resetting gradients
        self.optimizer.zero_grad()
        #  making predictions
        predictions = self.community(pictures)
        #  computing loss
        loss = loss_function(predictions, labels)
        log_dict['training_loss_per_batch'].append(loss.merchandise())
        train_losses.append(loss.merchandise())
        #  computing gradients
        loss.backward()
        #  updating weights
        self.optimizer.step()
      with torch.no_grad():
        print('deriving coaching accuracy...')
        #  computing coaching accuracy
        train_accuracy, train_recall, train_precision = accuracy(self.community, train_loader)
        log_dict['training_accuracy_per_epoch'].append(train_accuracy)
        log_dict['training_recall_per_epoch'].append(train_recall)
        log_dict['training_precision_per_epoch'].append(train_precision)

      #  validation
      print('validating...')
      val_losses = []

      #  setting convnet to analysis mode
      self.community.eval()

      with torch.no_grad():
        for pictures, labels in tqdm(val_loader):
          #  sending information to system
          pictures, labels = pictures.to(system), labels.to(system)
          #  making predictions
          predictions = self.community(pictures)
          #  computing loss
          val_loss = loss_function(predictions, labels)
          log_dict['validation_loss_per_batch'].append(val_loss.merchandise())
          val_losses.append(val_loss.merchandise())
        #  computing accuracy
        print('deriving validation accuracy...')
        val_accuracy, val_recall, val_precision = accuracy(self.community, val_loader)
        log_dict['validation_accuracy_per_epoch'].append(val_accuracy)
        log_dict['validation_recall_per_epoch'].append(val_recall)
        log_dict['validation_precision_per_epoch'].append(val_precision)

      train_losses = np.array(train_losses).imply()
      val_losses = np.array(val_losses).imply()

      print(f'training_loss: {spherical(train_losses, 4)}  training_accuracy: '+
      f'{train_accuracy}  training_recall: {train_recall}  training_precision: {train_precision} *~* validation_loss: {spherical(val_losses, 4)} '+  
      f'validation_accuracy: {val_accuracy}  validation_recall: {val_recall}  validation_precision: {val_precision}n')
      
    return log_dict

  def predict(self, x, eval=True):
    if eval:
      with torch.no_grad():
        return self.community(x)
    else:
      with torch.no_grad():
        self.community.prepare()
        return self.community(x)

Mannequin Coaching

The Lenet-5 structure is outlined as a member of the ‘ConvolutionalNeuralNet()’ class and is educated for 10 epochs with parameters as outlined within the code cell beneath.

mannequin = ConvolutionalNeuralNet(LeNet5_Dropout())

#  coaching mannequin and deriving metrics
log_dict = mannequin.prepare(nn.CrossEntropyLoss(), epochs=10, batch_size=64, 
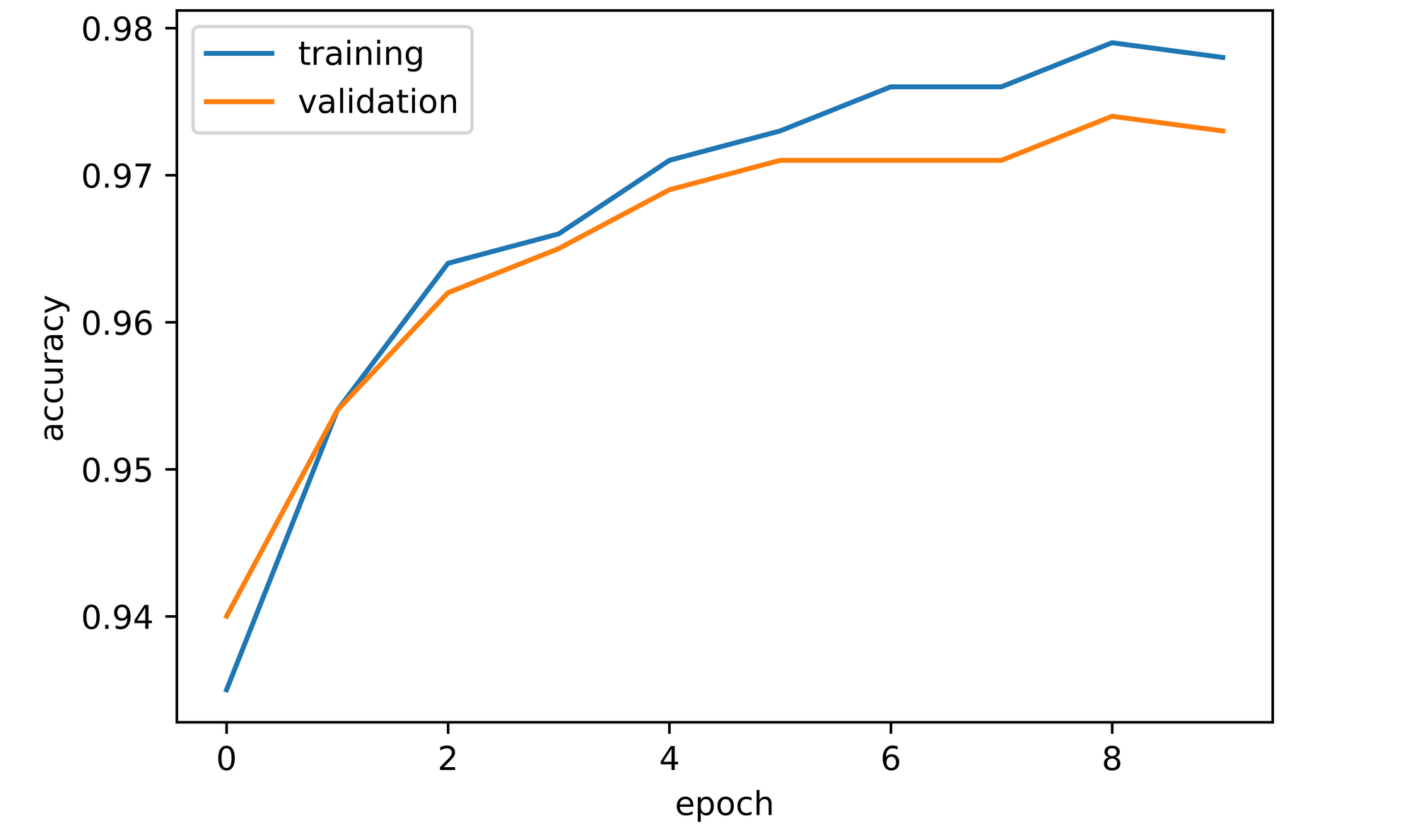
                           training_set=training_set, validation_set=validation_set)

From the accuracy plots, it may be seen that each coaching and validation accuracy improve over the course of mannequin coaching. Coaching accuracy peaked at a worth of just below 98% by the tenth epoch, whereas validation accuracy attained a worth of roughly 97.3% on the identical level.

Bayesian Inference

With the mannequin educated, it’s now time to make some Bayesian inference in a bid to see how assured our mannequin is about it is classifications. From exploring the dataset, I’ve recognized two pictures from the dataset with one being a typical determine 8 and one other being a bizarre trying determine 8 which I’ve deemed to be an edge case within the class of 8s.

These pictures will be discovered at index 61 and 591 respectively. For the sake of suspense I can’t be revealing which is which for now.

#  extracting two pictures from the validation set
image_1 = validation_set[61]
image_2 = validation_set[591]

The beneath outlined perform takes in a mannequin, a picture and a desired variety of fashions for Bayesian inference as parameters. The perform then returns a depend plot of the classification made by all of the fashions as analysis is turned off and dropout is saved in place.

def epistemic_check(mannequin, picture, model_number=20):
  """
  This mannequin returns a depend plot of mannequin classifications
  """
  confidence = []

  for i in vary(model_number):
    confidence.append(torch.argmax(F.softmax(mannequin.predict(picture.to(system), 
                                                           eval=False), dim=1)).merchandise())

  return sns.countplot(x=confidence)

Picture 1

Using the perform and setting variety of fashions to 100, we carry out inference on image_1. From the plot returned it’s seen that of all 100 fashions used to categorise the picture, solely a hand-full of them mistook the picture as a determine 2 with over 90% of them classifying the picture as a determine 8. A pointer to the truth that the mannequin is kind of sure about this picture.

epistemic_check(mannequin, image_1[0], 100)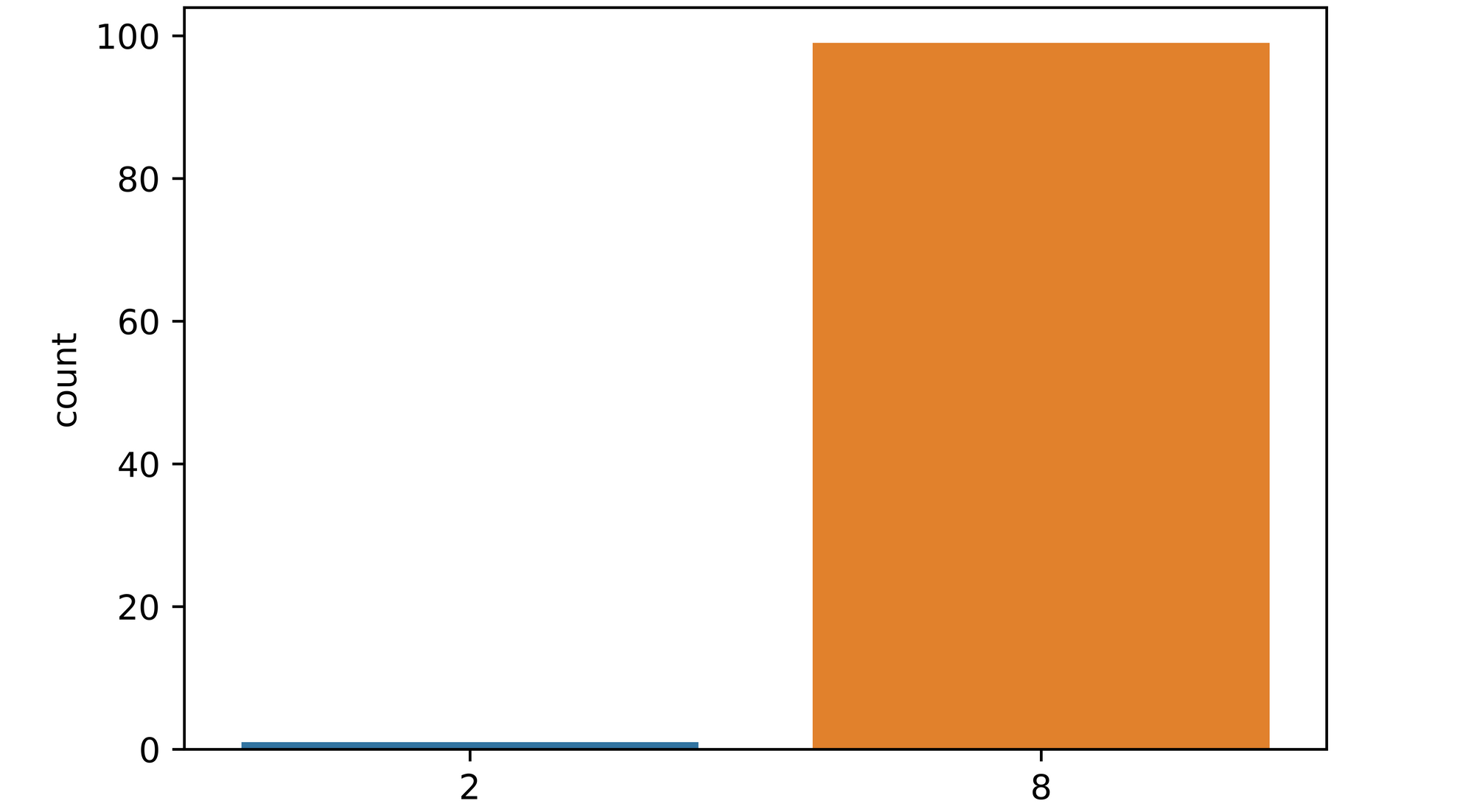

Visualizing the picture, we are able to see that it seems to be like a typical determine 8 and as such must be simply classifiable by the mannequin.

Picture 2

Passing image_2 to the perform and preserving all different parameters the identical yields some slightly attention-grabbing outcomes. From the plot returned, it may be seen {that a} important proportion of the 100 fashions (over 40) mistook the picture to be that of a determine 3, whereas about 4 fashions mistook the picture as both a 7 or a 9. Not like the primary picture, the fashions are primarily in disagreement over what the picture truly is, a pointer to epistemic uncertainty.

epistemic_check(mannequin, image_2[0], 100)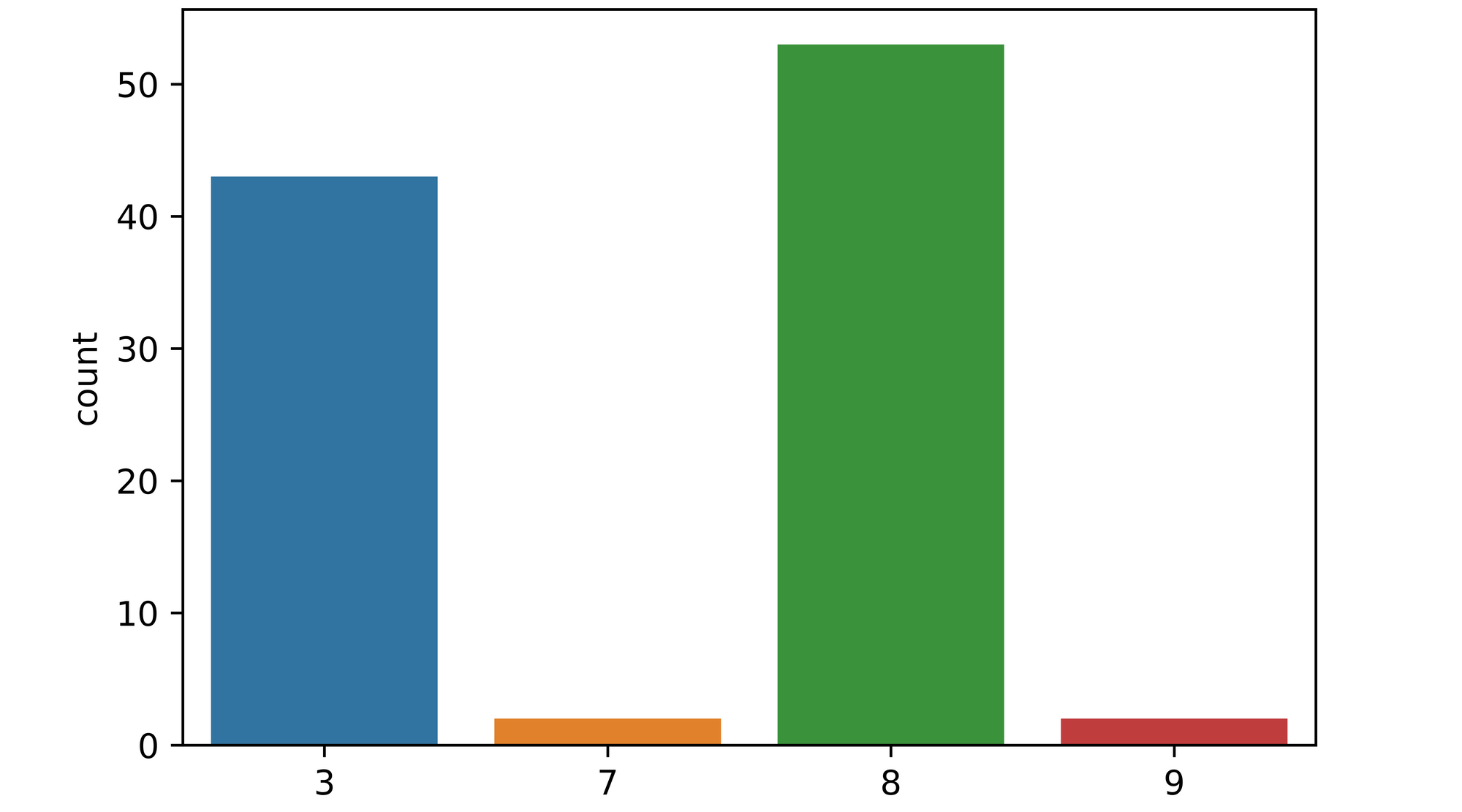

Trying on the picture, it may be appear that it’s fairly peculiar one because it does in-fact resemble a determine 3 in some lights regardless that it has been labeled as a determine 8 within the dataset.

On this article, we explored a broad overview of epistemic uncertainty in deep studying classifiers. Though we didn’t discover find out how to quantify this type of uncertainty, we had been in a position to develop an instinct about how an ensemble of fashions can be utilized to detect its presence for a selected picture occasion.