Introduction
In machine studying and synthetic intelligence, adversarial assaults have gained a lot consideration from researchers. These assaults alter the inputs to mislead the mannequin into making incorrect predictions. Amongst these, the Quick Gradient Signal Technique (FGSM), is especially value mentioning due to its effectiveness and ease .
The importance of FGSM lies in its capacity to reveal the vulnerability of recent fashions to minor variations in enter information. These perturbations, which steadily go unnoticed by human observers, inflict errors on prediction accuracy. Understanding and minimizing these vulnerabilities is pivotal to constructing fault-resistant machine studying methods trusted in sensible purposes like autonomous driving, healthcare provisioning, and safety administration.
This compelling article takes a deep dive into the which means of FGSM and elucidates its mathematical foundations with readability and precision. It offers demonstrations by an illustrative case research.
First-Order Taylor Enlargement in Adversarial Assaults
The utilization of the First-Order Taylor Enlargement approach in approximating the loss perform is a big technique to grasp how slight modifications in enter can have an effect on the loss in machine studying fashions. This strategy, significantly helpful when coping with adversarial assaults, entails computing an approximation of L(x+δ) utilizing its gradient with Taylor enlargement round x:
L(x+δ) ≈ L(x) + ∇L(x) ⋅ δ
- The loss on the authentic enter x is denoted as L(x), the gradient of the loss perform at x is represented by ∇L(x), and δ is a small perturbation to x.
- The route and price of the steepest improve of the loss perform is represented by ∇L(x). By perturbing x within the route of ∇L(x), we will predict how the loss perform will change.
Adversarial assaults use the Taylor Enlargement to seek out perturbations δ that maximize the loss perform L(x+δ). That is achieved by selecting δ proportional to the signal of ∇L(x):
δ = ϵ ⋅ signal(∇L(x))
the place ϵ is a small scalar controlling the magnitude of the perturbation.
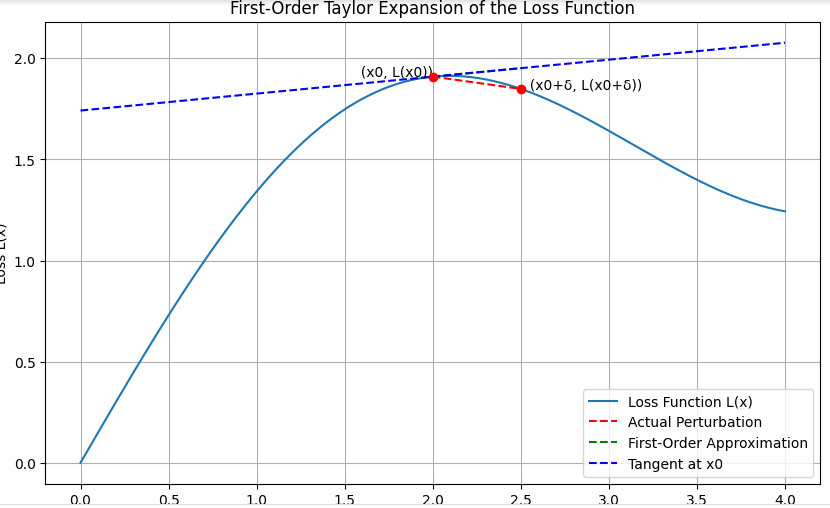
For illustration objective, let’s draw a diagram to signify the First-Order Taylor Enlargement of the loss perform. This may embody the loss curve, the unique level, the gradient vector, the perturbed level, and the first-order approximation.
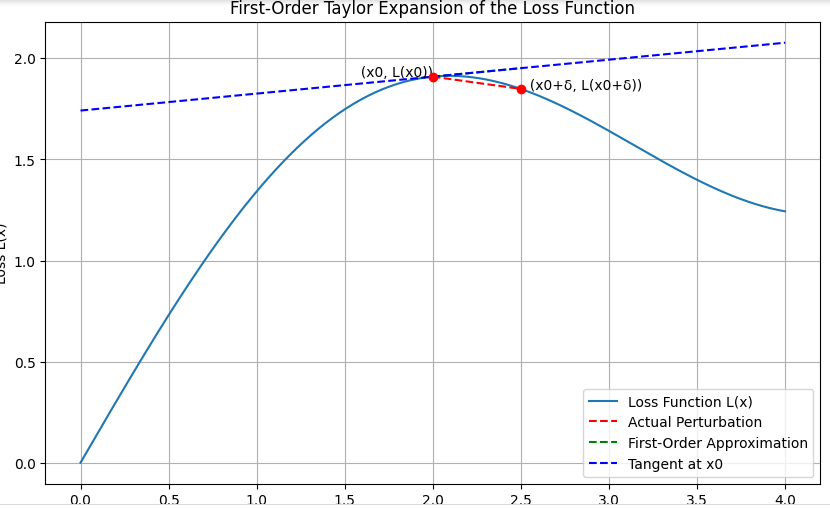
The diagram generated illustrates the important thing ideas of the First-Order Taylor Enlargement of the loss perform. Listed here are the primary takeaways:
- Loss Curve (L(x)): A clean curve representing the loss perform over totally different inputs.
- Unique Level (x0, L(x0)): The purpose on the loss curve which corresponds to the worth of the enter x0.
- Gradient Vector (∇L(x0)): This represents the slope of the tangent line on the level L(x0).
- Perturbed Level (x0 + δ, L(x0 + δ)): The brand new level after including a small perturbation δ to the enter x0.
- First-Order Approximation (L(x0) + ∇L(x0) ⋅ δ): The linear approximation of the loss perform round x0.
We are able to see how the gradient of the loss perform can be utilized to approximate the change in loss resulting from small perturbations within the enter. This understanding is essential for producing adversarial examples within the context of adversarial assaults.
The Quick Gradient Signal Technique (FGSM) is predicated on the precept of utilizing the gradients of the loss perform with respect to the enter information to find out the route by which the enter needs to be modified to extend the mannequin’s error. The steps concerned in FGSM may be described within the picture under:
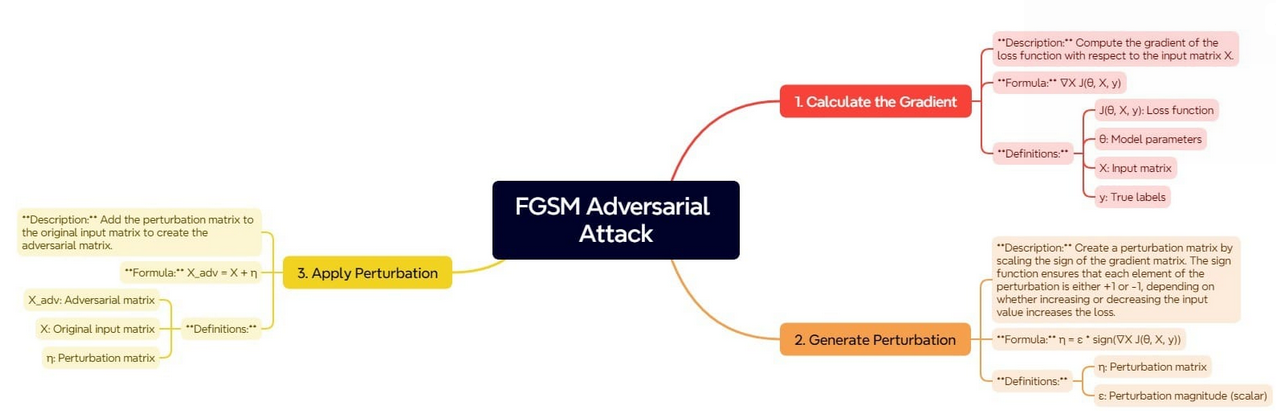
This course of begins by figuring out the gradient of the loss perform with respect to the enter information. The gradient defines how the loss perform would change if the enter information had been barely modified. Understanding this relationship, we will outline the route by which small shifts in inputs will improve the loss.
As soon as the gradient is computed, the following step is to generate the perturbation. That is achieved by scaling the signal of the gradient. The signal perform ensures that every element of the perturbation matrix is both + or – 1. This means whether or not the loss is most delicate to a rise or a lower of the corresponding enter worth.
The scaling issue ensures that these perturbations needs to be small however giant sufficient to idiot the mannequin.
The final step is to generate the adversarial instance by making use of this perturbation to the unique enter. By including the perturbation matrix to the unique enter matrix, we get the enter that appears similar to the unique information however is constructed to mislead the mannequin into making incorrect predictions.
Makes use of and Significance of FGSM in Machine Studying
Let’s think about some objective for which we will use Quick Grdient Sigh Technique:
- Testing Mannequin Robustness: FGSM is uded to evaluate machine studying mannequin resilience by testing it in opposition to adversarial assaults. This helps determine and repair potential vulnerabilities to enter information modifications.
- Enhancing Mannequin Safety:Sturdy fashions are key in safety apps like self-driving, healthcare, and finance. FGSM exams mannequin power by exposing vulnerability to assaults. Very important for safety-critical purposes with reliance on dependable fashions.
- Adversarial Coaching: It helps in adversarial coaching, bettering mannequin robustness by exposing it to potential assaults throughout coaching. This enhances its efficiency on perturbed inputs.
- Understanding Mannequin Habits: FGSM helps perceive mannequin conduct throughout enter perturbations, resulting in improved design and coaching for dependable methods.
- Benchmarking Adversarial Protection Strategies: It’s utilized by researchers to match protection strategies in opposition to adversarial assaults for growing strong safety.
- Benchmarking Adversarial Protection Strategies: It exposes vulnerabilities in methods like picture recognition and pure language processing, driving growth of safer ML purposes throughout industries.
- Academic Functions: It is usually used for schooling, serving as a fundamental introduction to adversarial assaults and defenses in machine studying. Understanding FGSM offers people with foundational information of extra superior strategies, permitting them to contribute to the sector.
Sensible Implementation
To exemplify the Quick Gradient Signal Technique (FGSM) assault virtually, we are going to use TensorFlow to generate adversarial examples. We are going to use Gradio as an interactive show device to showcase the outcomes. We’ll use a picture of a yellow Labrador retriever, which may be discovered right here.
First, let’s load the required libraries and the picture:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import gradio as gr
import requests
from PIL import Picture
from io import BytesIO
# Load the picture
image_url = "https://storage.googleapis.com/obtain.tensorflow.org/example_images/YellowLabradorLooking_new.jpg"
response = requests.get(image_url)
img = Picture.open(BytesIO(response.content material))
img = img.resize((224, 224))
img = np.array(img) / 255.0
# Show the picture
plt.imshow(img)
plt.present()
Output:
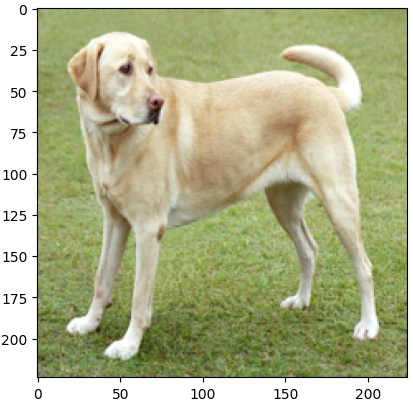
The above Python code helps to load and think about a picture from a selected URL through the use of frameworks reminiscent of TensorFlow, NumPy, Matplotlib, and PIL. It makes use of the requests library to fetch the picture, resizes it to a 224*224, and normalizes the worth of pixels between 0 and 1, earlier than changing the picture right into a numpy array.
Lastly, customers can show the picture and make sure the program appropriately hundreds and processes the picture.
Subsequent, let’s load a pre-trained mannequin and outline the FGSM assault perform:
# Load a pre-trained mannequin
mannequin = tf.keras.purposes.MobileNetV2(weights="imagenet")
# Outline the FGSM assault perform
def fgsm_attack(picture, epsilon):
picture = tf.convert_to_tensor(picture, dtype=tf.float32)
picture = tf.expand_dims(picture, axis=0)
with tf.GradientTape() as tape:
tape.watch(picture)
prediction = mannequin(picture)
loss = tf.keras.losses.categorical_crossentropy(tf.keras.utils.to_categorical([208], 1000), prediction)
gradient = tape.gradient(loss, picture)
signed_grad = tf.signal(gradient)
adversarial_image = picture + epsilon * signed_grad
adversarial_image = tf.clip_by_value(adversarial_image, 0, 1)
return adversarial_image.numpy().squeeze()
# Show the adversarial picture
adversarial_img = fgsm_attack(img, epsilon=0.08)
plt.imshow(adversarial_img)
plt.present()ouput:
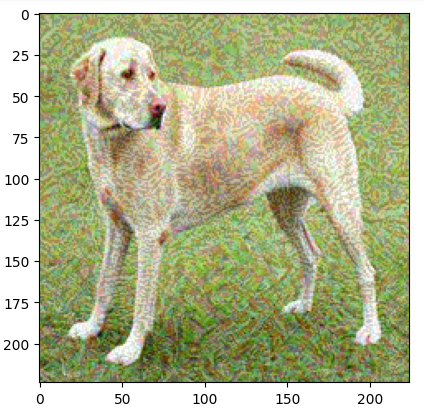
The code above demonstrates the right way to use the FGSM adversarial assault on a picture. It begins by downloading a pre-train mobileNetV2 mannequin with Imagenet weights.
The fgsm_attack technique is then outlined to carry out the adversarial assault. It transforms the enter picture right into a tensor, performs the computational work to find out the mannequin’s prediction, and computes the loss with respect to the goal label.
Through the use of TensorFlow’s gradient tape, the loss with respect to the picture enter is computed, and its signal is used to create perturbation. That is added to the unique picture with a multiplicative issue of epsilon to get an adversarial picture. The adversarial picture is then clipped to stay within the legitimate pixel vary.
Lastly, let’s combine this with Gradio to permit interactive exploration of the adversarial assault:
# Outline the Gradio interface
def generate_adversarial_image(epsilon):
adversarial_img = fgsm_attack(img, epsilon)
return adversarial_img
interface = gr.Interface(
fn=generate_adversarial_image,
inputs=gr.Slider(minimal=0.0, most=0.1, worth=0.01, label="Epsilon"),
outputs=gr.Picture(sort="numpy", label="Adversarial Picture"),
dwell=True
)
# Launch the Gradio interface
interface.launch()Output
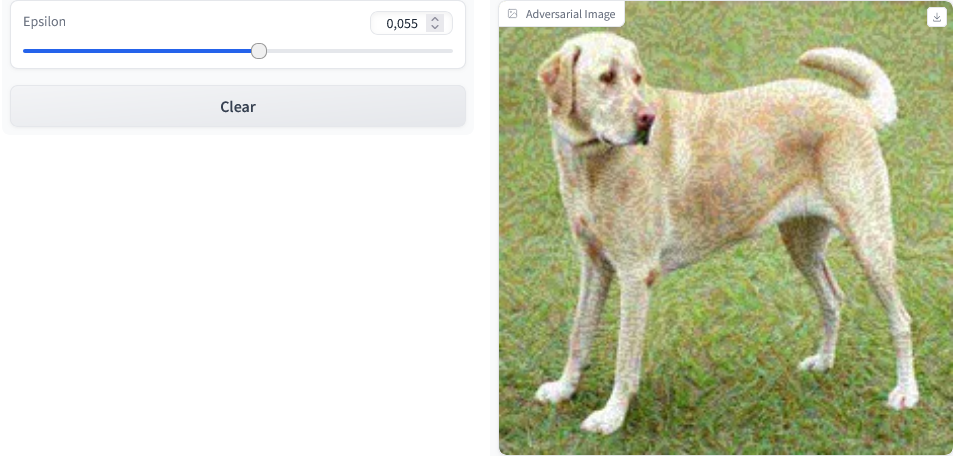
The code above generates a generate_adversarial_image perform. It accepts the epsilon worth as its parameter and executes the FGSM assault on the picture, then outputs the adversarial picture.
Our Gradio interface is personalized with a slider enter that permits for modification of the epsilon worth whereas additionally displaying updates in real-time through dwell=True parameter setting.
The command interface.launch() begins the web-based Gradio platform the place customers can manipulate numerous levels of values. This permits them to see corresponding adversarial photos generated by their inputs till they discover what fits them finest.
Comparability Between FGSM and Different Adversarial Assault Strategies
The desk under summarizes the comparability between FGSM and different adversarial assault strategies:
| Assault Technique | Description | Professionals | Cons |
|---|---|---|---|
| FGSM | Easy, environment friendly, makes use of gradient signal to generate adversarial examples | Fast, straightforward to implement, good for preliminary vulnerability evaluation | Produces simply detectable perturbations, much less efficient in opposition to strong fashions |
| PGD | Iterative model of FGSM, refines perturbations over a number of steps | Simpler at discovering adversarial examples, tougher to defend in opposition to | Computationally costly, time-consuming |
| CW | Carlini & Wagner assault, minimizes perturbations to be much less detectable | Very efficient, produces minimal perturbations | Complicated to implement, computationally intensive |
| DeepFool | Finds minimal perturbations to maneuver enter throughout resolution boundary | Produces small perturbations, efficient for a lot of fashions | Extra computationally costly than FGSM, much less intuitive |
| JSMA | Jacobian-based Saliency Map Assault, targets particular pixels for perturbation | Efficient at creating focused assaults, can management which pixels are modified | Complicated, may be gradual, requires detailed understanding of mannequin |
FGSM is most popular for quick computation and ease in finishing up preliminary robustness exams and adversarial studying. In distinction, to create highly effective adversarial examples, strategies reminiscent of PGD, or C&W can be utilized though they’re computationally costly. Strategies like DeepFool and JSMA are extra appropriate for observing minimal perturbations and have significance however devour extra computational energy.
Conclusion
This text explores the Quick Gradient Signal Technique (FGSM), a vital approach in adversarial machine studying. This technique exposes neural networks’ vulnerabilities to minor enter alterations by computing gradients with respect to the loss perform. The ensuing perturbations can drastically influence mannequin predictions. This makes understanding FGSM’s mathematical basis essential to creating resilient machine studying methods that do not buckle beneath assault. It is vital to imbue our vital purposes with a strong protection mechanism in opposition to such assaults.
The sensible implementation utilizing TensorFlow and Gradio illustrates FGSM’s real-world utility. Customers can simply tinker with various epsilon values to witness how these changes form adversarial picture output. Such an instance serves as a stark reminder of FGSM’s effectivity whereas equally underlining AI system vulnerability to malicious assaults. There’s a want for strong safety measures that assure optimum security and reliability in methods’ operations.
References
Adversarial instance utilizing FGSM
Adversarial Assaults and Defences: A Survey